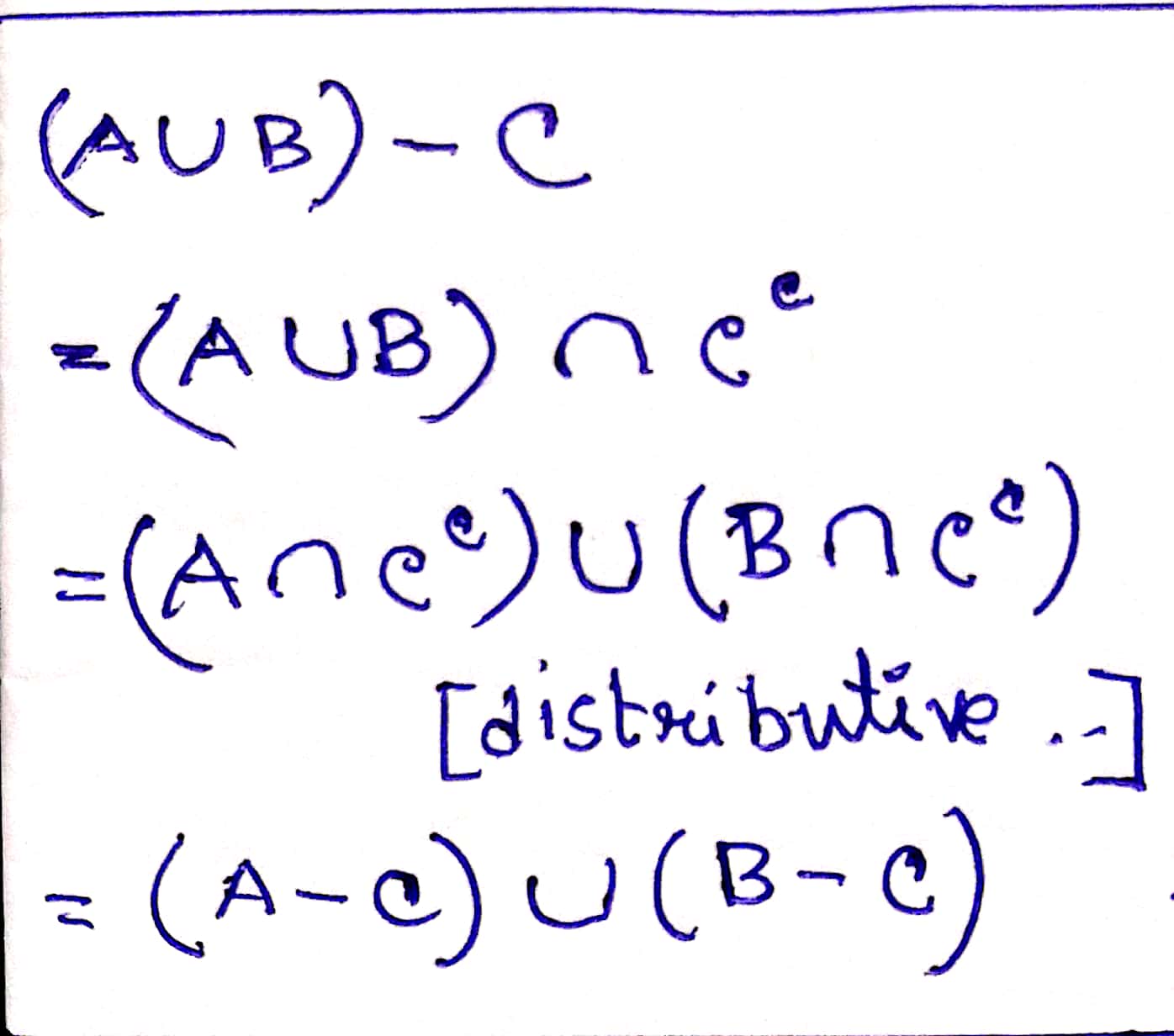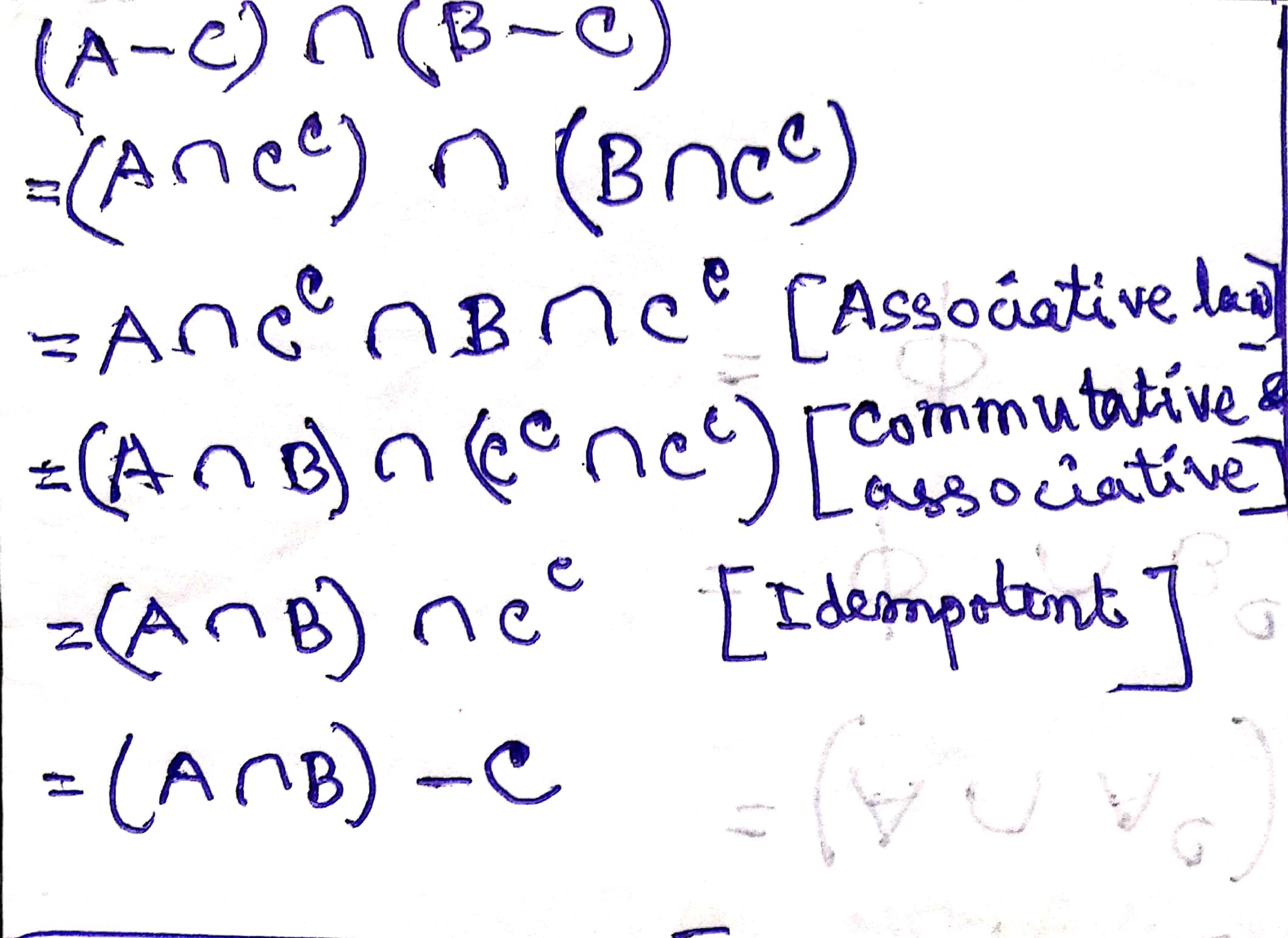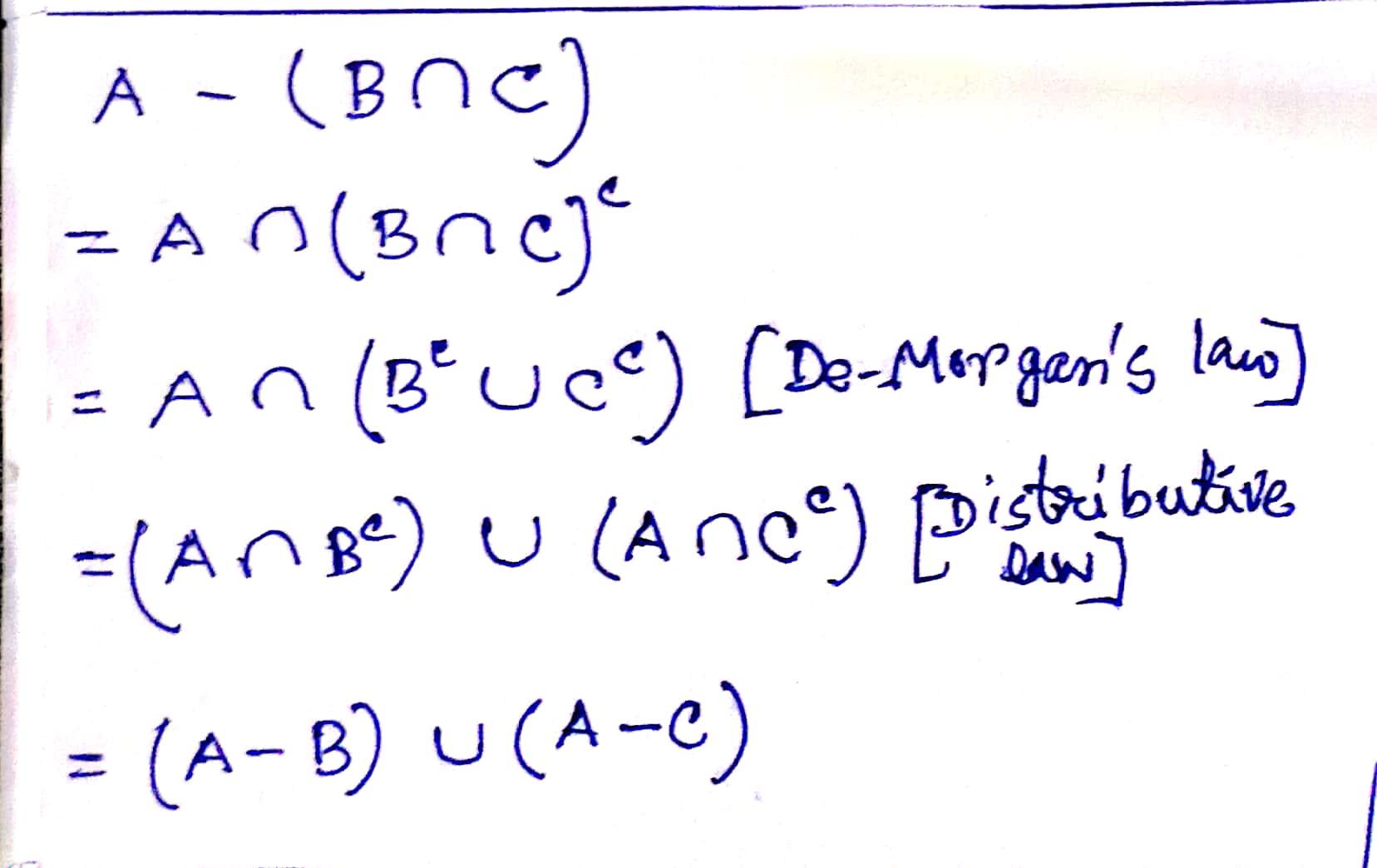For any three sets `A,B,C`, prove that -
(a) `A\cap(B-C)=(A\capB)-(A\capC)`
(b) `(A\cupB)-C=(A-C)\cup(B-C)`
(c) `(A\capB)-C=(A-C)\cap(B-C)`
(d) `A-(B\cupC)=(A-B)\cap(A-C)`
(e) `A-(B\capC)=(A-B)\cup(A-C)`
(f) `A-(B-C)=(A-B)\cup(A\capC)`