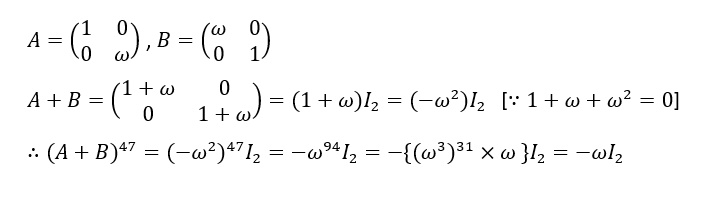If `\omega` is the imaginary cube root of 1 and $ A = \begin{pmatrix} 1 & 0 \\ 0 & \omega \end{pmatrix} $, $ B = \begin{pmatrix} \omega & 0 \\ 0 & 1 \end{pmatrix} $, then `(A+B)^47` is -- (a) `-I_2`, (b) `\omega\I_2`, (c) `-\omega^2I_2`, (d) `-\omega\I_2`