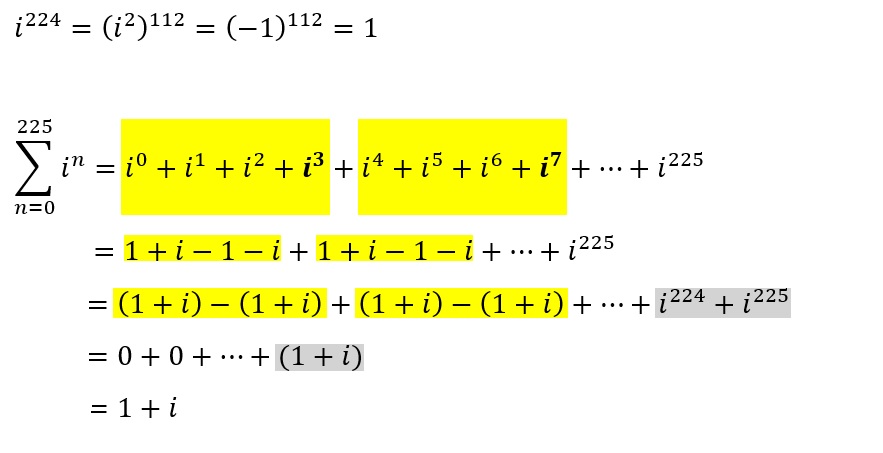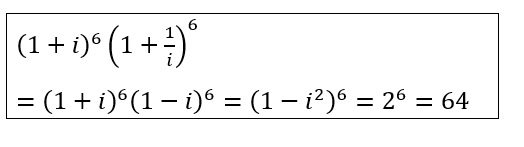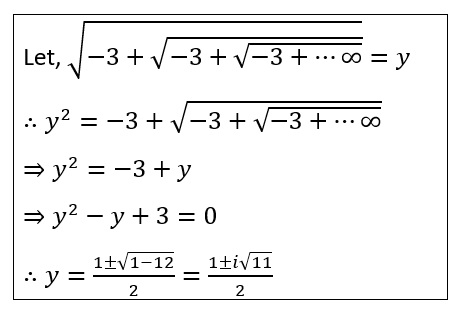Find the value of --
i) `1+i+i^2+i^3+i^4`
ii) `1+i^2+i^4+i^6+\cdots + i^16`
iii) `i^n + i^{n+1} + i^{n+2} + i^{n+3}` where `n \in \mathbb{N}`
iv) `\frac{i+i^2+i^3+i^4}{1+i}`
v) `\frac{i^2+i^4+i^6+i^7}{1+i^2+i^3}`
vi) `\sum_{n=0}^225 i^n`
vii) `(1+i)^6(1+1/i)^6`
viii) `\sqrt{-3 + \sqrt{-3 + \sqrt{-3 + \cdots \ \infty}}}`